gpssite.blogg.se - Speed of sound formula

But the music from all instruments arrives in cadence independent of distance, and so all frequencies must travel at nearly the same speed. Suppose that high-frequency sounds traveled faster-then the farther you were from the band, the more the sound from the low-pitch instruments would lag that from the high-pitch ones. The speed of sound in dry air at 20 C is 343 m/s and the lowest frequency sound wave that the human ear can detect is approximately 20 Hz.

If this independence were not true, you would certainly notice it for music played by a marching band in a football stadium, for example. This independence is certainly true in open air for sounds in the audible range of 20 to 20,000 Hz. One of the more important properties of sound is that its speed is nearly independent of frequency. The time for the echo to return is directly proportional to the distance. A bat uses sound echoes to find its way about and to catch prey. Figure 3 shows a use of the speed of sound by a bat to sense distances. By measuring the length of the air column (l) and the diameter of the tube (d) it is possible to calculate the speed of sound in air (c) using the formula. \boldsymbolit is 343 m/s, less than a 4% increase. The relationship of the speed of sound, its frequency, and wavelength is the same as for all waves: For objects traveling in dry air of a temperature of 20 ☌ (68 ☏) at sea level, this speed is approximately 343. Similar arguments hold that a large instrument creates long-wavelength sounds. Supersonic speed is the speed of an object that exceeds the speed of sound ( Mach 1). So a small instrument creates short-wavelength sounds. High pitch means small wavelength, and the size of a musical instrument is directly related to the wavelengths of sound it produces. The speed of sound is the distance travelled per unit of time by a sound wave as it propagates through an elastic medium.

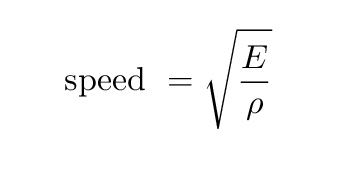
Small instruments, such as a piccolo, typically make high-pitch sounds, while large instruments, such as a tuba, typically make low-pitch sounds. The wavelength of sound is not directly sensed, but indirect evidence is found in the correlation of the size of musical instruments with their pitch. You can also directly sense the frequency of a sound. Air is a gas, and a very important property of any gas is the speed of. The flash of an explosion is seen well before its sound is heard, implying both that sound travels at a finite speed and that it is much slower than light. Computer Drawing of sound waves moving out from a bell. You can observe direct evidence of the speed of sound while watching a fireworks display. Sound, like all waves, travels at a certain speed and has the properties of frequency and wavelength.

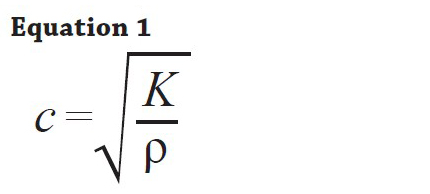
Sound travels more slowly than light does. When a firework explodes, the light energy is perceived before the sound energy. At 20 C (68 F), the speed of sound in air is about 343 metres per second (1,125 ft/s 1,235 km/h 767 mph 667 kn ), or one kilometre in 2.91 s or one mile in 4.69 s. Describe the effects of temperature on the speed of sound.įigure 1. The speed of sound is the distance travelled per unit of time by a sound wave as it propagates through an elastic medium.Describe the effects on the speed of sound as it travels through various media. The speed of sound in air, at sea level, at a temperature of 21 and under normal atmospheric conditions, is 341 ms1.

Describe the relationship between the speed of sound, its frequency, and its wavelength.

However at some point the molecules get close enough that the hard core repulsive interactions between molecules becomes important and from this pressure the gas starts getting "stiffer" again, which increases $v$ again. This difference increases as we increase the pressure, hence the negative gradient in your graph. At low pressures the attractions between the molecules dominate and the the gas is "floppier" than an ideal gas, which makes the velocity of sound lower than an ideal gas. What your diagram is telling you is that the gas is not ideal. That is:įor an ideal gas at constant temperature the velocity of sound does not depend on the pressure Since $\gamma$, $R$ and $M$ are constants equation (3) tells us that if we keep the temperature constant the velocity of sound is constant. The sound wave is described by: () its speed, () Its frequency (or. The speed of sound in an ideal gas is given by: The relation between speed of the sound wave (v) its frequency and wavelength () is v v. We know the formula to calculate speed of sound in air is cair 331.3 (1 + T/273.15) m/s for T in C Substituting the temperature value in the above formula we get the equation as follows cair 331.3 (1 + 35/273.15) m/s cair 351.8 m/s Therefore speed of sound in air for a temperatre of 35 C is 351.